chatGPT

Para ser honesto, chatGPT me tiene bien sorprendido, pero en realidad, si lo piensas bien, no me debería sorprender, no nos debería sorprender. La tecnología está evolucionando, abriendo nuevos caminos, logrando nuevos objetivos, todos los días. Y acercándonos al futuro: chatGPT ya está realmente cerca de la computadora abordo de la nave Enterprise en Star Trek y de Mother, en la nave Nostromo en la película Aliens. Una computadora amorosa que con paciencia infinita responde todas nuestras preguntas.

Pero siempre aparecen niños malcriados que le hacen la vida imposible a su mamá:

Chistes aparte, chatGPT puede responder cualquier cosa, siempre y cuando la respuesta exista en internet. Pero no nos ilusionemos: chatGPT no piensa, no deduce nada: es una matriz con una fórmula, que recibe una entrada y produce una salida, eso es todo. Es básicamente el mismo concepto de las redes neurales de hace 20 años, pero con matrices más sofisticadas y nuevas fórmulas. Nada más.

Se me presentó un problema bien difícil de resolver en estas semanas y no utilicé chatGPT para resolverlo. Mientras mi cerebro siga funcionando espero no necesitarla, Mother.

De matrices y parábolas

Y hablando de matrices, mis antíguas contendientes. Desde álgebra II se han encargado de hacerme la vida imposible. ¿Qué tengo yo que ver con matrices en estos días, más allá de las matrices de chatGPT ? Pues estoy programando un dungeon en khpx, y una de las fases es una batalla espacial, que en khpx es algo parecido a una batalla en Galaga o Galaxian (jugarlo en archive.org), juegos desconocidos hoy en día, provenientes de los albores de la computación cuando los juegos se jugaban en salas de juegos en cónsolas.

Es algo así como esto:

Los movimientos de las naves en este tipo de batallas lucen bien divertidos pero no necesariamente son algo fácil de implementar. Hay movimientos circulares que son fáciles de simular con la formula:

ship->lp.x = orig.x + ship->altitud.x * sin(ship->ang.x);
ship->lp.y = orig.y + ship->altitud.y * cos(ship->ang.x);

Pero otros movimientos son más complejos. En general, como aprendemos en 4to grado los cometas se mueven alrededor del sol en un movimiento parabólico, llamado así porque la curva que describe el cometa es una parábola:

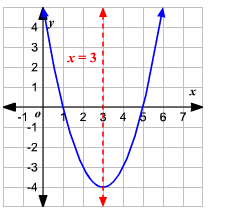
Lo que me llevó regresar a mis notas sobre cómo simular un movimiento parabólico, a ecuaciones con senos y cosenos y finalmente a matrices, a Cramer, etc. Haciendo corto el cuento largo, al final el código quedó parecido a algo como lo siguiente:

void getParabolaFormula(D3DXVECTOR2 p1, D3DXVECTOR2 p2, D3DXVECTOR2 p3, D3DXVECTOR3& result)
{
	D3DXMATRIX m0(
		1.0f, 1.0f, 1.0f, 0.0f,
		4.0f, 2.0f, 1.0f, 0.0f,
		1.0f, -1.0f, 1.0f, 0.0f,
		0.0f, 0.0f, 0.0f, 0.0f);

	// fill the data using the parabola formula
	// y = a*x^2+b*x+c

	D3DXMATRIX m(
		p1.x*p1.x, p1.x, 1.0f, 0.0f,
		p2.x*p2.x, p2.x, 1.0f, 0.0f,
		p3.x*p3.x, p3.x, 1.0f, 0.0f,
		0.0f, 0.0f, 0.0f, 0.0f);

	D3DXVECTOR3 r(p1.y, p2.y, p3.y);

	// calculate the determinant
	// D3DXMatrixDeterminant and  D3DXMatrixInverse doesn't work out the box
	// d = a(ei-fh)-b(di-fg)+c(dh.eg)
	float d = m._11 * (m._22 * m._33 - m._23 * m._32) -
		m._12 * (m._21 * m._33 - m._23 * m._31) +
		m._13 * (m._21 * m._32 - m._22 * m._31);
	g_write_debug("determinant %6.2f ", d);

	D3DXMATRIX Da(m), Db(m), Dc(m);

	Da._11 = r.x; Da._21 = r.y; Da._31 = r.z;
	Db._12 = r.x; Db._22 = r.y; Db._31 = r.z;
	Dc._13 = r.x; Dc._23 = r.y; Dc._33 = r.z;

	float da, db, dc;

	da = Da._11 * (Da._22 * Da._33 - Da._23 * Da._32) -
		Da._12 * (Da._21 * Da._33 - Da._23 * Da._31) +
		Da._13 * (Da._21 * Da._32 - Da._22 * Da._31);


	db = Db._11 * (Db._22 * Db._33 - Db._23 * Db._32) -
		Db._12 * (Db._21 * Db._33 - Db._23 * Db._31) +
		Db._13 * (Db._21 * Db._32 - Db._22 * Db._31);

	dc = Dc._11 * (Dc._22 * Dc._33 - Dc._23 * Dc._32) -
		Dc._12 * (Dc._21 * Dc._33 - Dc._23 * Dc._31) +
		Dc._13 * (Dc._21 * Dc._32 - Dc._22 * Dc._31);

	result.x = da / d; result.y = db / d; result.z = dc / d;


}

Esta función recibe 3 puntos que se encuentran en una parábola y devuelve la fórmula de la parábola. Se supone que esto debe devolver a, b, y c para resolver la siguiente fórmula:

y = a x2 + b x + c

Pero no funcionó. Pasé varios días tratando de encontrar el problema pero no lo logré. He pensado que el problema no está en estas matrices, sino en el código que utiliza la función. Como ya tengo años en khpx y no puedo seguir dedicándole tiempo a cosas que no tienen nada que ver con programación de juegos (falso, todo tiene que ver con programación de juegos) empecé a buscar otra solución.

En realidad yo no necesito tres puntos o mejor dicho, yo no tengo tres puntos, yo tengo dos puntos, el punto donde está la nave enemiga y el punto donde está khpx. Y el punto donde está khpx, es el vértice de la parábola (el sol, en nuestro ejemplo del cometa y el sol):

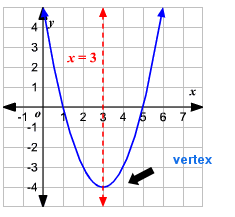
Esta vez la ecuación es mucho pero mucho pero mucho más sencilla y no necesitamos odiosas matrices. Mi cuaderno terminó lleno de fórmulas con ejemplos:

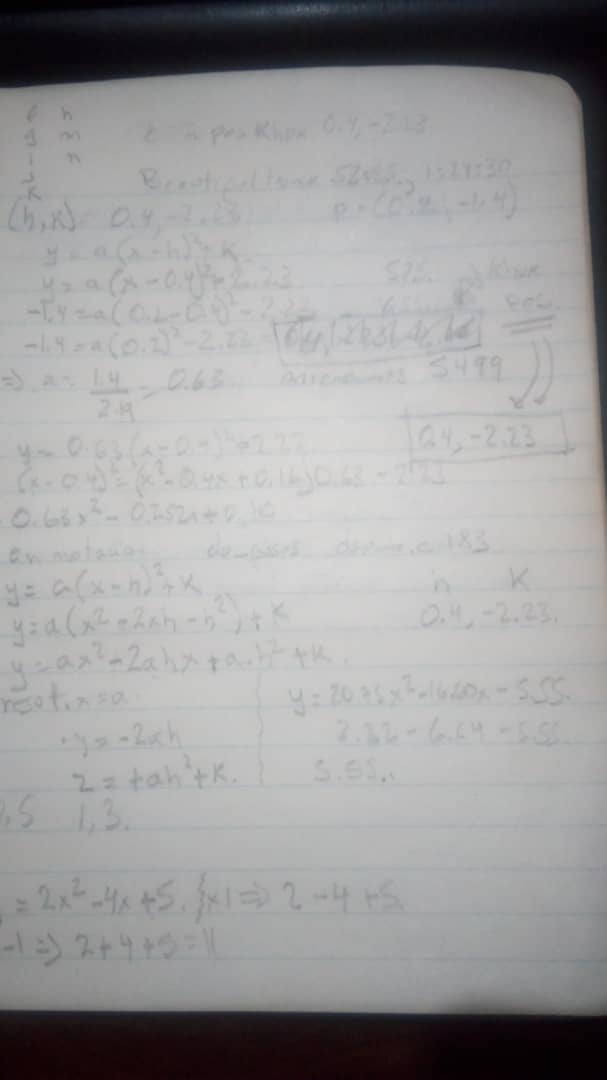
Pero el resultado fue bien siemple, tan simple como la siguiente función:

void getParabolaFormula2(D3DXVECTOR2 p, D3DXVECTOR2 vertex, D3DXVECTOR3& result)
{
	float h = vertex.x;
	float k = vertex.y;
	float a = (p.y - k) / POW2(p.x - h);
	result.x = a;
	result.y = -2 * a * h;
	result.z = a * h * h + k;
}

Esta función recibe los dos puntos y devuelve a, b c como en el caso anterior para resolver la ecuación de la curva. Lo cual me permitió implementar lo siguiente:

Como un primer borrador no está tan mal. Le faltan los misiles de khpx, la coraza protectora (o campo de lasers), las secuencias de destrucción de las naves, y un largo etc. Espero terminarlo en dos semanas un mes dos meses (mentira).

Estaba pensando que este dungeon debe estar en el primer demo de khpx, para comenzar desde el comienzo a ponerle algo de acción al juego. Se cansa uno.